Numerical simulations of nonlinear progressive waves are prone to developing spurious high-frequency standing waves unless the flow field is given sufficient time to adjust (Dommermuth, 2000). An adjustment scheme allows the natural development of nonlinear self-wave (locked modes) and inter-wave (free modes) interactions.
For High-Order Spectral (HOS) simulations, an adjustment procedure allows nonlinear free-surface simulations to be initialized with linear solutions. For two-phase volume-of-fluid simulations like the Numerical Flow Analysis (NFA) code, nonlinear waves are generated from rest by gradually applying a surface stress. NFA requires a different approach than HOS because the necessary two-phase solutions for progressive waves are not readily available. Dommermuth, Fu, O’Shea, Brucker, and Wyatt (2010) show that the adjustment procedure can be used to initialize fully-nonlinear simulations of regular waves and irregular seas. The paper is available at http://tinyurl.com/yaedzwqe.
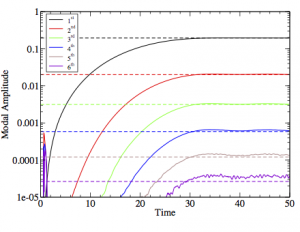
The figure below shows an adjusted NFA solution in comparison to an exact Stokes wave up to the sixth harmonic. Note that there are no oscillations in the Fourier harmonics.
Deike, Popinet, and Melville (2015), Deike, Melville, and Popinet (2016), and Deike, Pizzo, and Melville (2017) use third-order Stokes solutions to initialize their two-phase VOF simulations. As discussed by Dommermuth (2000) and Dommermuth, et al. (2010), third-order Stokes solutions lead to the formation of spurious high-frequency standing waves for simulations of both regular waves and irregular seas and are inappropriate for fully-nonlinear simulations of waves. The gradual application of a surface stress (see Dommermuth, et al., 2010) eliminates problems with initializing two-phase VOF simulations with third-order solutions.
References:
Dommermuth, D. G. (2000) The initialization of nonlinear waves using an adjustment scheme, Wave Motion, 32, 307–317.
Dommermuth, D. G., Fu, T. C., O’Shea, T. T., Brucker, K. A., and Wyatt, D. C., (2010) Numerical prediction of a seaway, Proceedings of the 28th Symposium on Naval Hydrodynamics, Pasadena, California, USA.
Deike, L., S. Popinet, and W. Melville (2015), Capillary effects on wave breaking, J. Fluid Mech., 769, 541–569.
Deike, L., W. Melville, and S. Popinet (2016), Air entrainment and bubble statistics in breaking waves, J. Fluid Mech., 801, 91–129.
Deike, L., Pizzo, N. E., and Melville, W. K. (2017) Lagrangian transport by breaking surface waves. J. Fluid Mech. (submitted).
